Заседание 65 (28 декабря 2001 г.)
Довбыш С. А.
Оптимальные ляпуновские метрики гомеоморфизмов, обладающих гиперболической
структурой.
Пусть
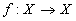 - гомеоморфизм компактного
метрического пространства
- гомеоморфизм компактного
метрического пространства 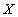 с метрикой
с метрикой
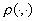 ,
локальные (радиуса
,
локальные (радиуса
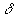 )
устойчивое
)
устойчивое 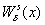 и неустойчивое
и неустойчивое
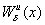 “многообразия” точки
“многообразия” точки
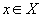 определяются как
определяются как
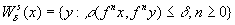 ,
,
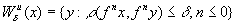 .
.
Определение.
Гомеоморфизм
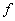 обладает гиперболической структурой (ГС), а метрика
обладает гиперболической структурой (ГС), а метрика
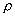 называется гиперболической, если существуют такие
называется гиперболической, если существуют такие
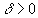 ,
,
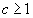 и
и
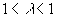 , что
, что
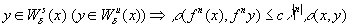 (1)
(1)
при
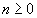 (
(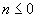 ). Метрика
называется ляпуновской, если при этом
). Метрика
называется ляпуновской, если при этом
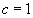 .
.
Пусть
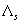 и
и 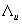 есть точные нижние грани для констант
есть точные нижние грани для констант
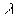 таких, что при подходящих
таких, что при подходящих
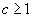 выполнены
неравенства (1), относящиеся, соответственно, к устойчивым и неустойчивым многообразиям.
Константы
выполнены
неравенства (1), относящиеся, соответственно, к устойчивым и неустойчивым многообразиям.
Константы 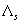 и
и 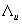 не изменятся при выборе меньшего радиуса
не изменятся при выборе меньшего радиуса
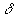 локальных многообразий.
локальных многообразий.
К. Сакаи доказал (Sakai K. Topology and Appl. 1995. V. 63, no. 3.
P. 263--266; 2001. V. 112, no. 3. P. 229--243), что у гомеоморфизма
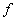 , обладающего ГС, имеется ляпуновская метрика, эквивалентная
исходной (т. е. определяющая ту же топологию), причем эту метрику можно выбрать так, что
оба отображения
, обладающего ГС, имеется ляпуновская метрика, эквивалентная
исходной (т. е. определяющая ту же топологию), причем эту метрику можно выбрать так, что
оба отображения 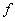 и
и 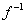 будут липшицевыми относительно нее. Следующая теорема
утверждает существование оптимальных
ляпуновских метрик.
будут липшицевыми относительно нее. Следующая теорема
утверждает существование оптимальных
ляпуновских метрик.
Теорема.
Пусть гомеоморфизм 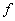 обладает ГС и
обладает ГС и
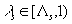 ,
, 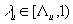 . Тогда ляпуновскую метрику
. Тогда ляпуновскую метрику
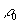 можно выбрать так, что
можно выбрать так, что
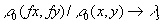 (и,
соответственно,
(и,
соответственно, 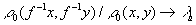 ) равномерно по всем
) равномерно по всем
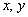 таким,
что
таким,
что 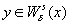 (соответственно,
(соответственно,
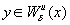 ) при
) при
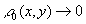 или, что равносильно, при
или, что равносильно, при
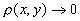 . Более того,
отображение
. Более того,
отображение 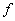 (соответственно,
(соответственно,
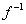 ) будет липшицевым
относительно
) будет липшицевым
относительно 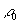 с постоянной
с постоянной
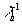 (соответственно,
(соответственно, 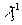 ), если
), если
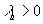 (
(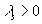 ).
).
В случае, когда
гомеоморфизм
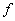 дополнительно обладает локальной структурой произведения, т. е.
удовлетворяет аксиоме
дополнительно обладает локальной структурой произведения, т. е.
удовлетворяет аксиоме 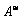 (см. Алексеев В. М. Символическая динамика // Одиннадцатая
матем. школа. Киев: Ин-т матем. АН УССР, 1976. 210 с.) метрика
(см. Алексеев В. М. Символическая динамика // Одиннадцатая
матем. школа. Киев: Ин-т матем. АН УССР, 1976. 210 с.) метрика
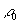 в малых масштабах приблизительно
представляется как прямая сумма метрик, соответствующих
каноническим координатам,
а малые участки “
многообразий”
в малых масштабах приблизительно
представляется как прямая сумма метрик, соответствующих
каноническим координатам,
а малые участки “
многообразий”
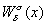 ,
, 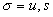 (рассмотренные при надлежащем увеличении) приблизительно
являются в некотором смысле
``плоскими'' подмножествами
(рассмотренные при надлежащем увеличении) приблизительно
являются в некотором смысле
``плоскими'' подмножествами
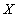 .
.
![]() - гомеоморфизм компактного
метрического пространства
- гомеоморфизм компактного
метрического пространства ![]() с метрикой
с метрикой
![]() ,
локальные (радиуса
,
локальные (радиуса
![]() )
устойчивое
)
устойчивое ![]() и неустойчивое
и неустойчивое
![]() “многообразия” точки
“многообразия” точки
![]() определяются как
определяются как ![]() ,
,
![]() .
. ![]() (1)
(1)