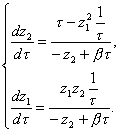В работе изучаются вопросы интегрируемости через конечный набор элементарных функций неконсервативных динамических систем следующего вида:

            , .

Система задана на , , где функции , , таковы:

            , ,

            , .

Такая система соответствует системе , которая заменой  приводится к виду , где , .

            Пусть функции  () – полиномы по .

            Рассмотрим для начала случай систем на . Например, следующим системам

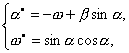             и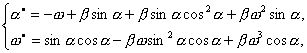  

в других переменных () сопоставим уравнения

             и , соответственно.

            В случае же  следующая система

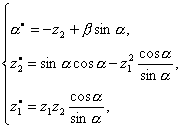
возникающая при описании пространственного движения тела в сопротивляющейся среде, соответствует следующей системе: